C/C++ HPC CUDA

基于 CUDA 并行的通用矩阵乘法 2/2

GEMM with CUDA 2/2

Posted by lzzmm on December 31, 2021
About 10 minutes to read

DCS293 - High Performance Computing 2021 Fall

前言

本文通过 NVDIA 的矩阵计算函数库 cuBLAS 计算矩阵相乘，并进行性能比较与分析；使用滑窗法和在 GPU 上进行直接卷积和 im2col 方法卷积；使用 cuDNN 进行卷积并比较性能。

实验环境

Linux jupyter-zhamao 5.4.0-74-generic #83~18.04.1-Ubuntu SMP

Intel(R) Xeon(R) Gold 6242 CPU @ 2.80GHz 16 cores 32 processors

NVIDIA Tesla V100-SXM2-32GB × 4

  • Driver Version: 440.33.0
  • CUDA Version: 10.2

cuBLAS

cuBLAS 在 CUDA6.0 中出现，现在包含2个类 API，常规 cuBLAS，简称为 cuBLAS API，另外一种是 CUBLASXT API。使用 cuBLAS 的时候，应用程序应该分配矩阵或向量所需的 GPU 内存空间，并加载数据，调用所需的 cuBLAS 函数，然后从 GPU 的内存空间上传计算结果至主机，cuBLAS API 也提供一些帮助函数来从 GPU 中写或者读取数据。

通过 NVDIA 的矩阵计算函数库 cuBLAS 计算矩阵相乘，矩阵规模从512增加至8192。

cuBLAS 默认按照列优先原则存储矩阵。根据 $(B^TA^T)^T = AB$ 我们对输入和计算结果进行转置即可。但是我发现他的函数里面已经可以通过参数控制是否转置 A 和 B，还是很厉害的。

cuBLAS中能用于运算矩阵乘法的函数有4个，分别是 cublasSgemm（单精度实数）、cublasDgemm（双精度实数）、cublasCgemm（单精度复数）、cublasZgemm（双精度复数）。这里使用 cublasSgemm ，它的定义（在 cublas_v2.h 和 cublas_api.h 中）如下。

0
1
2
3
4
5
6
7
8
9
10
11

#define cublasSgemm cublasSgemm_v2
CUBLASAPI cublasStatus_t CUBLASWINAPI cublasSgemm_v2
(
    cublasHandle_t handle,
    cublasOperation_t transa, cublasOperation_t transb,
    int m, int n, int k,
    const float *alpha,
    const float *A, int lda,
    const float *B, int ldb,
    const float *beta,
    float *C, int ldc
);

该函数实际上是用于计算 C = α A B +β C 的，其中 $A_{m×k}$ 、$B_{k×n}$ 、$C_{m×n}$ 为矩阵，α 、β 为标量。在此处 α = 1，β = 0.

首先需要使用 cuBLAS 库

0

#include <cublas_v2.h>

下面初始化三个矩阵和先前的代码相同，把矩阵发给设备和计算如下：

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

cublasHandle_t handle;
    cublasStatus_t status = cublasCreate(&handle);

    if (status != CUBLAS_STATUS_SUCCESS) {
        if (status == CUBLAS_STATUS_NOT_INITIALIZED) {
            printf("cuBLAS 对象实例化出错\n");
        }
        getchar();
        return EXIT_FAILURE;
    }

    float *cuda_A, *cuda_B, *cuda_C;
    cudaMalloc((void **)&cuda_A, sizeof(float) * MATRIX_SIZE * MATRIX_SIZE);
    cudaMalloc((void **)&cuda_B, sizeof(float) * MATRIX_SIZE * MATRIX_SIZE);
    cudaMalloc((void **)&cuda_C, sizeof(float) * MATRIX_SIZE * MATRIX_SIZE);

    cublasSetVector(
        MATRIX_SIZE * MATRIX_SIZE, // 要存入显存的元素个数
        sizeof(float),             // 每个元素大小
        A,                         // 主机端起始地址
        1,                         // 连续元素之间的存储间隔
        cuda_A,                    // GPU 端起始地址
        1                          // 连续元素之间的存储间隔
    );
    cublasSetVector(
        MATRIX_SIZE * MATRIX_SIZE, // 要存入显存的元素个数
        sizeof(float),             // 每个元素大小
        B,                         // 主机端起始地址
        1,                         // 连续元素之间的存储间隔
        cuda_B,                    // GPU 端起始地址
        1                          // 连续元素之间的存储间隔
    );

    // 同步函数
    // cudaError_t cudaThreadSynchronize() is deprecated [-Wdeprecated-declarations]
    // cudaThreadSynchronize();
    cudaDeviceSynchronize();

    float alpha = 1;
    float beta = 0;

    cublasSgemm(
        handle,      // blas 库对象
        CUBLAS_OP_T, // 矩阵 A 属性参数
        CUBLAS_OP_T, // 矩阵 B 属性参数
        MATRIX_SIZE, // A, C 的行数
        MATRIX_SIZE, // B, C 的列数
        MATRIX_SIZE, // A 的列数和 B 的行数
        &alpha,      // 运算式的 α 值
        cuda_A,      // A 在显存中的地址
        MATRIX_SIZE, // lda
        cuda_B,      // B 在显存中的地址
        MATRIX_SIZE, // ldb
        &beta,       // 运算式的 β 值
        cuda_C,      // C 在显存中的地址(结果矩阵)
        MATRIX_SIZE  // ldc
    );

    // 同步函数
    // cudaThreadSynchronize();
    cudaDeviceSynchronize();

    cublasGetVector(
        MATRIX_SIZE * MATRIX_SIZE, // 要取出元素的个数
        sizeof(float),             // 每个元素大小
        cuda_C,                    // GPU 端起始地址
        1,                         // 连续元素之间的存储间隔
        C,                         // 主机端起始地址
        1                          // 连续元素之间的存储间隔
    );

    clock_t endTime = clock();
    // C^T
    cToR(C, MATRIX_SIZE, MATRIX_SIZE);

    clock_t endTime2 = clock();

cudaThreadSynchronize() 建议换成 cudaDeviceSynchronize()

编译记得加上 -lcublas

MatrixSize Time [转置后(转置前)] blockSize = 32 blockSize = 512
512 0.444934s (0.440606s) 0.2052s 0.2213s
1024 0.483945s (0.467051s) 0.2137s 0.2214s
2048 0.625998s (0.518511s) 0.2380s 0.2356s
4096 0.979877s (0.536048s) 0.4239s 0.3105s
8192 3.677618s (1.129133s) 1.4426s 0.4903s

CUBLAS 可能转置 A 和 B 有一定开销，所以就算结果不经过转置也比任务1的实现慢许多。

尝试不转置 A 和 B 把 CUBLAS_OP_T 改为 CUBLAS_OP_N。

不转置的话确实快一点。但是还是比 block size = 512 的要慢。我写的程序在访存的时候显然没有使用共享内存，时延较高，但是却和 cublas 不相上下甚至比它快。可能是显卡性能强劲的原因。

CUDA CNN

在信号处理、图像处理和其他工程/科学领域，卷积是一种使用广泛的技术。在深度学习领域，卷积神经网络(CNN)这种模型架构就得名于这种技术。在本实验中，我将在 GPU 上实现卷积操作，注意这里的卷积是指神经网络中的卷积操作，与信号处理领域中的卷积操作不同，它不需要对 Filter 进行翻转，不考虑 bias。

通过CUDA实现直接卷积（滑窗法），输入从256增加至4096或者输入从32增加至512.

输入：Input和Kernel(3x3)

问题描述：用直接卷积的方式对Input进行卷积，这里只需要实现2D, height*width，通道channel(depth)设置为3，Kernel (Filter)大小设置为3*3*3，个数为3，步幅(stride)分别设置为1，2，3，可能需要通过填充(padding)配合步幅(stride)完成CNN操作。注：实验的卷积操作不需要考虑bias(b)，bias设置为0.

输出：输出卷积结果以及计算时间

对于结果矩阵中的每一个位置创建一个线程与之计算对应，并且为了防止产生数据依赖，每个线程需要将位置的所有 Chanel 中需要累加的值完全计算，得出完整的值。

首先我们还是一个处理单元计算输出矩阵的一个元素。根据输入矩阵和滤波器参数来确定补0和输出矩阵大小。

image-20211231230416684

0
1
2
3
4
5
6

const int zeroPadding = (FILTER_SIZE - 1) / 2;
const int in2DSize = MATRIX_SIZE + 2 * zeroPadding;
const int out2DSize = (MATRIX_SIZE - FILTER_SIZE + 2 * zeroPadding) / STRIDE + 1;

dim3 blockSize(BLOCK_SIZE, BLOCK_SIZE);
dim3 gridSize((out2DSize + blockSize.x - 1) / blockSize.x,
              (out2DSize + blockSize.y - 1) / blockSize.y);

然后申请矩阵空间，与任务一相似。

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14

float *hInMat = (float *)malloc(sizeof(float) * MATRIX_CHANNEL * in2DSize * in2DSize);
float *hKernel = (float *)malloc(sizeof(float) * MATRIX_CHANNEL * FILTER_SIZE * FILTER_SIZE);
float *hOutMat = (float *)malloc(sizeof(float) * MATRIX_CHANNEL * out2DSize * out2DSize);

srand(0);
for (int d = 0; d < MATRIX_CHANNEL; d++) {
    for (int i = zeroPadding; i < in2DSize - zeroPadding; i++) {
        for (int j = zeroPadding; j < in2DSize - zeroPadding; j++) {
            hInMat[d * in2DSize * in2DSize + i * in2DSize + j] = (float)rand() / RAND_MAX;
        }
    }
}
for (int i = 0; i < MATRIX_CHANNEL * FILTER_SIZE * FILTER_SIZE; i++) {
    hKernel[i] = (float)rand() / RAND_MAX;
}

开始计时，申请设备上显存空间然后把数据复制过去。代码省略。

然后开始计算卷积。

0
1
2
3
4
5

CONV2D<<<gridSize, blockSize, 0>>>
(dInMat, dKernel, dOutMat,
 in2DSize, out2DSize,
 MATRIX_CHANNEL,
 FILTER_NUM, FILTER_SIZE,
 STRIDE, zeroPadding);

核函数如下：

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

// CUDA kernel function
__global__
void CONV2D(const float *input, const float *kernel, float *output, const int in2DSize, const int out2DSize, const int depth, const int K, const int f, const int stride, const int zeroPadding) {
    const int row = threadIdx.y + blockIdx.y * blockDim.y;
    const int col = threadIdx.x + blockIdx.x * blockDim.x;

    if (row < out2DSize && col < out2DSize) {
        for (int c = 0; c < depth; c++) {
            output[idx(c, row, col, out2DSize)] = 0.0f;
            int x = row * stride;
            int y = col * stride;
            for (int k = 0; k < K; k++) {
                for (int i = 0; i < f; i++) {
                    for (int j = 0; j < f; j++) {
                        output[idx(c, row, col, out2DSize)] += input[idx(k, x + i, y + j, in2DSize)] * kernel[idx(k, i, j, f)];
                    }
                }
            }
        }
    }
    return;
}
MatrixSize Time [S = 1] Time [S = 2] Time [S = 3]
512 0.207790s 0.215431s 0.210600s
1024 0.224814s 0.218759s 0.217814s
2048 0.309920s 0.296813s 0.225991s
4096 0.451333s 0.367948s 0.318341s
8192 0.913531s 0.574979s 0.521228s

使用 im2col 方法结合 GEMM 实现卷积操作

用im2col的方式对Input进行卷积，这里只需要实现2D, height*width，通道channel(depth)设置为3，Kernel (Filter)大小设置为3*3*3，个数为3。

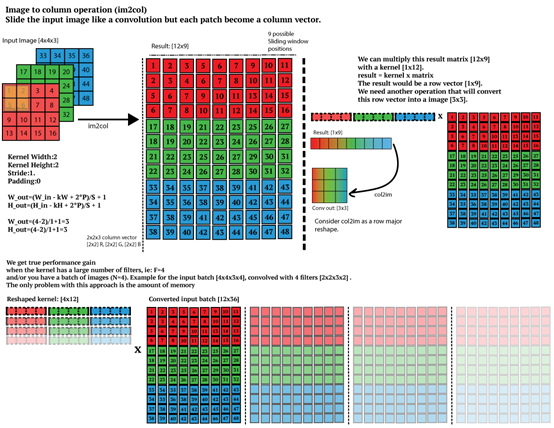
image-20211231230901943

根据步长、卷积核大小等信息将输入矩阵由3D转换为2D，将卷积核变成一维向量。数个卷积核向量拼成矩阵与输入矩阵Matrix(2D)相乘，即可得到结果。

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

// im2col

// Mat3D2Mat2D
dx[9] = {-1, 0, 1, -1, 0, 1, -1, 0, 1};
dy[9] = {-1, -1, -1, 0, 0, 0, 1, 1, 1};
for (int d = 0; d < MATRIX_CHANNEL; d++) {
    for (int i = 0; i < in2DSize; i++) {
        for (int j = 0; j < in2DSize; j++) {
            int x = i * STRIDE;
            int y = j * STRIDE;
            for (int k = 0; k < FILTER_SIZE * FILTER_SIZE; k++) {
                hInMat2D[idx2(d * FILTER_SIZE * FILTER_SIZE + k, i * in2DSize + j, in2DSize * in2DSize)] = hInMat3D[idx3(d, x + dx[k], y + dy[k], in2DSize)];
            }
        }
    }
}

// kernel3D2Mat2D
for (int k = 0; k < FILTER_NUM; k++) {
    for (int d = 0; d < MATRIX_CHANNEL; d++) {
        for (int i = 0; i < FILTER_SIZE; i++) {
            for (int j = 0; j < FILTER_SIZE; j++) {
                hKernel2D[idx2(k, (d * FILTER_SIZE * FILTER_SIZE + i * FILTER_SIZE + j), MATRIX_CHANNEL * FILTER_SIZE * FILTER_SIZE)] = hKernel3D[idx3(k, i, j, FILTER_SIZE)];
            }
        }
    }
}

使用 cuDNN 提供的卷积方法进行卷积操作

NVIDIA cuDNN 是用于深度神经网络的 GPU 加速库。它强调性能、易用性和低内存开销。

cuDNN 中计算卷积操作的由cudnnConvolutionForward()来实现，其原型为

0
1
2
3
4
5
6
7
8
9
10
11
12
13

cudnnStatus_t CUDNNWINAPI cudnnConvolutionForward(
    cudnnHandle_t                       handle,
    const void                         *alpha,
    const cudnnTensorDescriptor_t       xDesc,
    const void                         *x,
    const cudnnFilterDescriptor_t       wDesc,
    const void                         *w,
    const cudnnConvolutionDescriptor_t  convDesc,
    cudnnConvolutionFwdAlgo_t           algo,
    void                               *workSpace,
    size_t                              workSpaceSizeInBytes,
    const void                         *beta,
    const cudnnTensorDescriptor_t       yDesc,
    void                               *y );

首先使用库

0

#include <cudnn.h>

然后创建 cudnn 句柄和上下文句柄，然后分别定义输入的张量，卷积核，输出的张量的大小需要使用 cudnnGetConvolution2dForwardOutputDim() 来获得。最后使用 cudnnConvolutionForward() 来完成计算。

0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

// Compile: nvcc -I /opt/conda/include/ -L /opt/conda/lib/ -lcudnn cudnn.cu -o cudnn
// Run:     export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/opt/conda/lib/
//          ./ cudnn

#include <cuda.h>
...

int main() {
    ...
    clock_t startTime = clock();

    cudnnStatus_t status;
    cudnnHandle_t cudnn_handle;
    cudnnCreate(&cudnn_handle);

    clock_t startTime2 = clock();

    cudnnTensorDescriptor_t matrixDesc;
    cudnnCreateTensorDescriptor(&matrixDesc);
    cudnnSetTensor4dDescriptor(matrixDesc, CUDNN_TENSOR_NCHW, CUDNN_DATA_FLOAT, 1, MATRIX_CHANNEL, MATRIX_SIZE, MATRIX_SIZE);
    float *dInMat;
    cudaMalloc(&dInMat, sizeof(float) * MATRIX_CHANNEL * MATRIX_SIZE * MATRIX_SIZE);
    cudaMemcpy(dInMat, hInMat, sizeof(float) * MATRIX_CHANNEL * MATRIX_SIZE * MATRIX_SIZE, cudaMemcpyHostToDevice);

    cudnnFilterDescriptor_t kernelDesc;
    cudnnCreateFilterDescriptor(&kernelDesc);
    cudnnSetFilter4dDescriptor(kernelDesc, CUDNN_DATA_FLOAT, CUDNN_TENSOR_NCHW, FILTER_NUM, MATRIX_CHANNEL, FILTER_SIZE, FILTER_SIZE);

    float *dKernel;
    cudaMalloc(&dKernel, sizeof(float) * FILTER_NUM * MATRIX_CHANNEL * FILTER_SIZE * FILTER_SIZE);
    cudaMemcpy(dKernel, hKernel, sizeof(float) * FILTER_NUM * MATRIX_CHANNEL * FILTER_SIZE * FILTER_SIZE, cudaMemcpyHostToDevice);

    cudnnConvolutionDescriptor_t convDesc;
    cudnnCreateConvolutionDescriptor(&convDesc);
    cudnnSetConvolution2dDescriptor(convDesc, 1, 1, 1, 1, 1, 1, CUDNN_CROSS_CORRELATION, CUDNN_DATA_FLOAT);
    int outN, outC, outH, outW;

    cudnnGetConvolution2dForwardOutputDim(convDesc, matrixDesc, kernelDesc, &outN, &outC, &outH, &outW);

    cudnnTensorDescriptor_t outputDesc;
    cudnnCreateTensorDescriptor(&outputDesc);
    cudnnSetTensor4dDescriptor(outputDesc, CUDNN_TENSOR_NCHW, CUDNN_DATA_FLOAT, outN, outC, outH, outW);

    float *dOutMat;
    cudaMalloc(&dOutMat, sizeof(float) * outN * outC * outH * outW);
    float *hOutMat = (float *)malloc(sizeof(float) * outN * outC * outH * outW);

    cudnnConvolutionFwdAlgo_t algo;
    cudnnGetConvolutionForwardAlgorithm(cudnn_handle, matrixDesc, kernelDesc, convDesc, outputDesc, CUDNN_CONVOLUTION_FWD_PREFER_FASTEST, 0, &algo);

    size_t workspace_size = 0;
    cudnnGetConvolutionForwardWorkspaceSize(cudnn_handle, matrixDesc, kernelDesc, convDesc, outputDesc, algo, &workspace_size);

    void *workspace;
    cudaMalloc(&workspace, workspace_size);

    float alpha = 1.0f;
    float beta = 0.0f;

    status = cudnnConvolutionForward(cudnn_handle, &alpha, matrixDesc, dInMat, kernelDesc, dKernel, convDesc, algo, workspace, workspace_size, &beta, outputDesc, dOutMat);

    cudnnDestroy(cudnn_handle);

    cudaMemcpy(hOutMat, dOutMat, sizeof(float) * outN * outC * outH * outW, cudaMemcpyDeviceToHost);

    cudaFree(dInMat);
    cudaFree(dKernel);
    cudaFree(dOutMat);

    clock_t endTime = clock();

    printf("Time cost = %fs (%fs)\n", (float)(endTime - startTime) / CLOCKS_PER_SEC, (float)(endTime - startTime2) / CLOCKS_PER_SEC);

    free(hInMat);
    free(hKernel);
    free(hOutMat);

    return 0;
}

测试发现在构建 cudnn 句柄和上下文句柄的时候耗时十分漫长，计算时间很短。

各种方法的比较

MatrixSize Time [CONV] Time [im2col] cuDNN
512 0.210600s 0.200572s 1.564251s (0.008061s)
1024 0.217814s 0.210927s 1.382498s (0.018986s)
2048 0.225991s 0.213380s 1.451955s (0.052267s)
4096 0.318341s 0.292239s 1.694651s (0.157581s)
8192 0.521228s 0.460625s 1.945823s (0.685741s)

im2col 比单纯的 cuda 卷积要快一点点，cuDNN 在申请句柄的时候花了许多时间，但是去除掉这部分时间的话会发现……矩阵规模小的时候很快，矩阵规模变大之后反而变慢了。

References

https://blog.csdn.net/fengbingchun/article/details/54691225

https://blog.csdn.net/sunmc1204953974/article/details/51098028

https://blog.csdn.net/dwyane12138/article/details/78449898

https://cs231n.github.io/convolutional-networks/

https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-convolutional-neural-networks

https://www.jianshu.com/p/3d925c2ef55e

Creative Commons License本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
CATALOG
    FEATURED TAGS
    漫谈 C/C++ HPC OS asm
    FRIENDS