DCS245 - Reinforcement Learning and Game Theory 2021 Fall
Cliff Walk
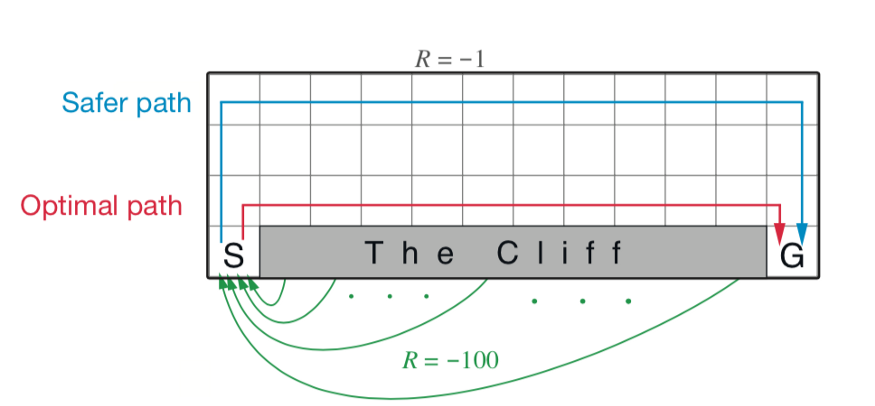
S是初始状态,G是目标状态,The Cliff是悬崖,走到那上面则回到起点。动作可以是向上下左右移动。假设不能移出划定的边界。碰到 The Cliff 则奖励-100,其余情况奖励-1,到 The Cliff 或 G 则结束。这是一个经典的二维网格游戏。
我们定义一个 State 类,用来表示当前的状态和回报。包含有初始化整个网格,维护网格,给出回报三个功能。
因为超过页数所以这段代码不是很重要,删了。
然后我们定义一下两种算法的玩家通用的一些功能。基于 $\epsilon$ - greedy 的方法选择方向如下:
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def chooseAction(self):
"""
return a random action or a greedy action
"""
# epsilon-greedy
mx_next_reward = -9999
action = ""
if np.random.uniform(0, 1) <= self.exp_rate:
action = np.random.choice(self.actions)
else:
# greedy action
for a in self.actions:
current_position = self.pos
next_reward = self.state_actions[current_position][a]
if next_reward >= mx_next_reward:
action = a
mx_next_reward = next_reward
return action
进行循环的主要框架如下:
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
while 1:
curr_state = self.pos
cur_reward = self.cliff.giveReward()
total_reward += cur_reward # this episode
action = self.chooseAction()
# next position
self.cliff.pos = self.cliff.nextPosition(action)
self.pos = self.cliff.pos
self.states.append([curr_state, action, cur_reward]) # S, A, R
if self.cliff.end:
break
for a in self.actions:
self.state_actions[self.pos][a] = reward
# use SARSA or Q-learning to update
...
下面就是使用算法更新了。
Sarsa 算法

Sarsa 算法属于在线控制算法,它一直使用一个策略(ϵ-greedy)来更新价值函数和选择新的动作。在迭代的时候,我们首先基于 ϵ−greedy 在当前状态 $S$ 选择一个动作 $A$,这样系统会转到一个新的状态 $S’$ , 同时给我们一个即时奖励 $R$,在新的状态 $S’$,我们会基于ϵ−greedy在状态 $S’$ 选择一个动作 $A’$,但不执行动作 $A’$,只是用来更新的我们的价值函数,价值函数的更新公式是:

γ 是衰减因子,α 是迭代步长。
根据这个算法我们更新价值函数 $Q(S,A)$,也就是 self.state_actions
0
1
2
3
4
5
if self.sarsa:
for s in reversed(self.states):
pos, action, r = s[0], s[1], s[2]
current_value = self.state_actions[pos][action]
reward = current_value + self.lr * (r + reward - current_value)
self.state_actions[pos][action] = round(reward, 3)
Q-learning 算法

Q-learning 属于离线控制算法,它使用两个控制策略,一个策略用于选择新的动作,另一个策略用于更新价值函数。它的前两步和 Sarsa 算法一样,通过基于 ϵ−greedy 在当前状态 $S$ 选择一个动作 $A$,这样系统会转到一个新的状态 $S’$ , 同时给我们一个即时奖励 $R$,但是在新的状态并不选择新的动作,而是使用观察所有动作并选取最大值来学习。
0
1
2
3
4
5
6
7
else: # Q-learning
for s in reversed(self.states):
pos, action, r = s[0], s[1], s[2]
current_value = self.state_actions[pos][action]
reward = current_value + self.lr * (r + reward - current_value)
self.state_actions[pos][action] = round(reward, 3)
# update using the max value of S'
reward = np.max(list(self.state_actions[pos].values()))
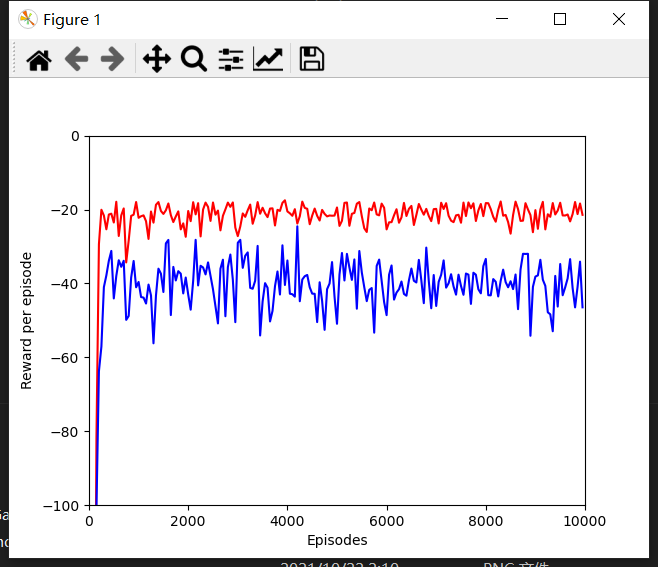
实验结果
学习率和贪婪系数都为 0.1 的时候运行一万次得出如下结果。


This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.