基于 Pthread 并行的通用矩阵乘法

DCS293 - High Performance Computing 2021 Fall

DCS242 - Parallel and Distributed Computing 2021 Fall

实验目的

构造 MPI 版本矩阵乘法加速比和并行效率表

分别构造MPI版本的标准矩阵乘法和优化后矩阵乘法（例如：集合通信、create_struct）的加速比和并行效率表格。并分类讨论两种矩阵乘法分别在强扩展和弱扩展情况下的扩展性。
通过 Pthreads 实现通用矩阵乘法

通过Pthreads实现通用矩阵乘法的并行版本，Pthreads并行线程从1增加至8，矩阵规模从512增加至2048.
基于 Pthreads 的数组求和
1. 写使用多个进程/线程对数组a[1000]求和的简单程序演示Pthreads的用法。创建n个线程，每个线程通过共享单元global_index获取a数组的下一个未加元素，注意不能在临界段外访问全局下标global_index
2. 重写上面的例子，使得各进程可以一次最多提取10个连续的数，以组为单位进行求和，从而减少对下标的访问
Pthreads 求解二次方程组的根

编写一个多线程程序来求解二次方程组𝑎𝑥2+𝑏𝑥+𝑐=0的根，使用下面的公式 $x = \frac{-b\pm \sqrt{b^2-4ac}}{2a}$ 中间值被不同的线程计算，使用条件变量来识别何时所有的线程都完成了计算
编写一个多线程程序来估算 $y=x^2$ 曲线与 x 轴之间区域的面积，其中 x 的范围为 [0,1] 。

实验过程和核心代码

0 构造 MPI 版本矩阵乘法加速比和并行效率表

	Order of Matrix
Comm_size	128	256	512	1024
1	0.02741s	0.17674s	1.83702s	77.17566s
2	1.178(0.02331s)	1.117(0.15843s)	1.217(1.50956s)	1.169(66.0327s)
4	0.274(0.10317s)	0.555(0.31888s)	1.258(1.46010s)	1.236(62.4365s)
8	0.208(0.13276s)	0.876(0.20205s)	1.213(1.51450s)	1.068(72.2826s)
16	0.054(0.51092s)	1.311(0.13487s)	0.892(2.06238s)	2.026(38.2236s)

表 1：MPI 版本的标准矩阵乘法

	Order of Matrix
Comm_size	128	256	512	1024
1	0.02741s	0.17674s	1.83702s	77.17566
2	2.092(0.01310s)	1.086(0.16273s)	1.664(1.10468s)	1.169(66.03279s)
4	2.362(0.01161s)	1.104(0.16028s)	2.602(0.70605s)	1.236(62.43645s)
8	0.187(0.14627s)	0.320(0.55185s)	1.530(1.20032s)	4.053(19.21622s)
16	0.073(0.37408s)	0.268(0.66055s)	2.161(0.84966s)	4.103(18.81658s)

表 2：集合通信优化后矩阵乘法

CPU: Intel Core i5 6200U 2c4t

第一张表，在矩阵规模为128时，数据量较少，通信时间为主要程序耗时的主要原因，当启用多个核心进行MPI通信时，通信时间甚至超过了计算时间，为程序耗时的主要原因，所以最终耗时反而有所增加。规模增加到1024的时候，可以看到多核计算效率逐步提高。当核心数再次增加8-16时，使用了 oversubscribe 超线程开始启用，效果必定没有8核、16核效果好，但还是有一定的优势，计算时间会减少一些。所以这个算法是弱可扩展的，它的加速必须随着矩阵规模增大。

第二张表，也是弱可扩展的，在增加进程的规模的时候必须增加矩阵规模才能保证加速比不下降。

由于我的CPU只有4个核，所以上面得出的结果比较局限。

1通过 Pthreads 实现通用矩阵乘法

详细实现见源码，此处展示大致框架。

...
// Compile: gcc -pthread -o GEMM_p GEMM_pthread.c
// Run:     ./GEMM_p
#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define THREAD_NUM 8
#define SIZE 512
#define AVG_ROWS (SIZE / THREAD_NUM)
...

float *A, *B, *C;
int    M = SIZE, N = SIZE, K = SIZE, m, n, k;

void  matrix_multiply(int M, int N, int K, float *A, float *B, float *C);
void  PrintMatrix(float *Matrix, const int R, const int C);
void *thread_GEMM(void *arg) {
    int num_of_thread = (int)arg;
    int start, end;
    start = AVG_ROWS * num_of_thread;
    end   = AVG_ROWS * (num_of_thread + 1) - 1;

    printf("Thread #%d: start:%d end:%d\n", num_of_thread, start, end);
    matrix_multiply(AVG_ROWS, SIZE, SIZE, A + (start * N), B, C + (start * K));

    pthread_exit(0);
}

int main() {
	...
    pthread_id = (pthread_t *)malloc(THREAD_NUM * sizeof(pthread_t));
	// initialize matrix A and B
	...
    for (i = 0; i < THREAD_NUM; i++) {
        pthread_create(pthread_id + i, NULL, thread_GEMM, i);
    }
    startTime = clock();
    for (i = 0; i < THREAD_NUM; i++) {
        pthread_join(pthread_id[i], NULL);
    }
    endTime = clock();
    printf("Total time: %lfs\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
	...
}
// Print the matrix
void PrintMatrix(float *Matrix, const int R, const int C) {
	...
}
void matrix_multiply(int M, int N, int K, float *A, float *B, float *C) {
	...
}

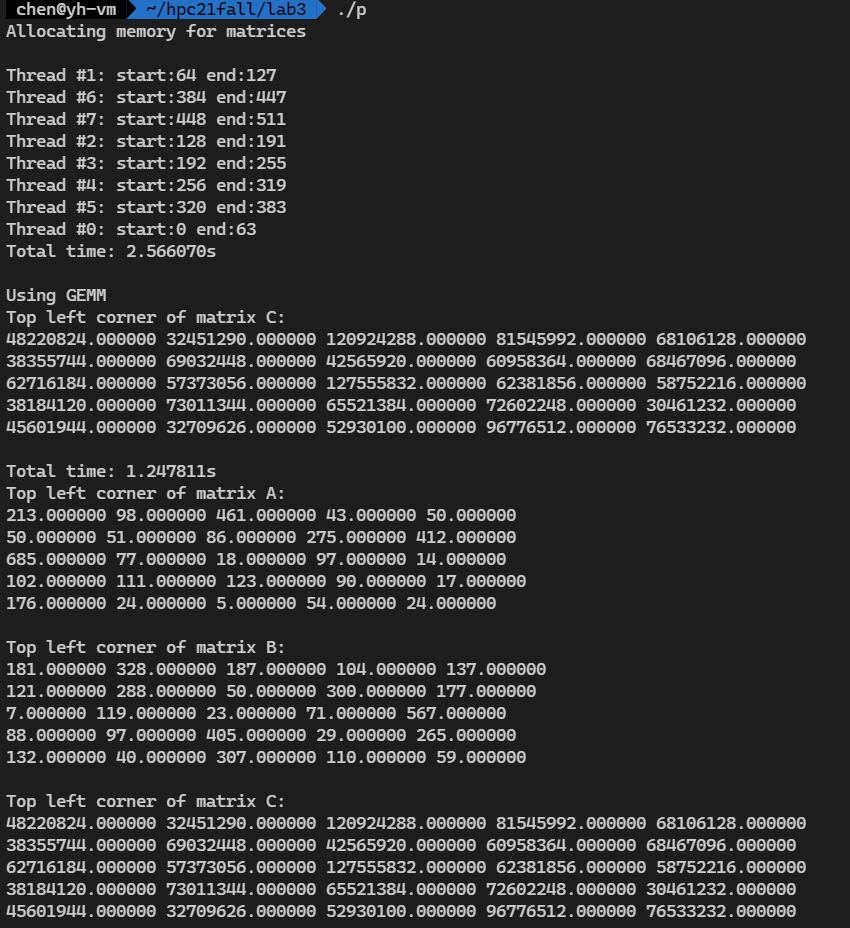
可以看到结果是正确的。

接下来分别测试时间。

线程数1，矩阵边长 512

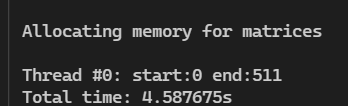
线程数2，边长 512

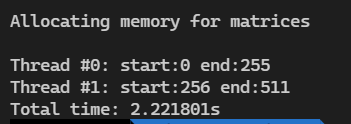
线程数4，边长512

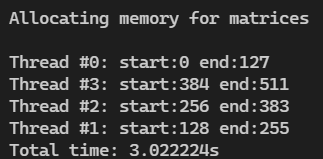
线程数8 边长512

线程数8 边长1024

线程数8 边长2048

2 基于 Pthreads 的数组求和

// array_sum_v1.c

// Copyright (c) 2021 CHEN Yuhan
// Date: 2021-19-27
//
// Computing sum using multi-threading
// Fetch 1 element each time
//
// Compile: gcc -pthread -o v1 array_sum_v2.c
// Run:     ./v1
#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define NUM 1000
#define RND 10
#define THREAD_NUM 10
#define FETCH_NUM 1

pthread_mutex_t mutex;

int          Array[NUM];
long long    sum[THREAD_NUM] = {0}; // = {0} 暂时保存线程执行结果
unsigned int global_index    = 0;

void* thread_sum(void* arg) {
    int       num_of_thread = (int)arg;
    long long start;
    while (global_index < NUM) {
        pthread_mutex_lock(&mutex);
        if (global_index < NUM)
            start = global_index;
        else
            pthread_exit(0);
        long long end = (start + FETCH_NUM) <= NUM ? start + FETCH_NUM - 1 : NUM - 1;
        global_index += end - start + 1;
        pthread_mutex_unlock(&mutex);

        long long i;

        for (i = start; i <= end; i++) {
            sum[num_of_thread] += Array[i];
        }
    }

    pthread_exit(0);
}

int main() {
    clock_t    start_time, end_time;
    pthread_t* pthread_id = NULL;
    long long  i;
    int        T      = RND;
    double     s_time = 0, p_time = 0;
    

    while (T--) {
        global_index       = 0;
        long long s_result = 0, p_result = 0;

        // Initialize Array
        for (i = 0; i < NUM; i++) {
            Array[i] = (int)(rand() / NUM);
        }

        printf("\nStart serial computing...\n");
        start_time = clock();
        for (i = 0; i < NUM; i++) {
            s_result += Array[i];
        }
        end_time = clock();

        s_time += (double)(end_time - start_time) / CLOCKS_PER_SEC;

        printf("\nSum of the array is %lld\n", s_result);

        pthread_id = (pthread_t*)malloc(THREAD_NUM * sizeof(pthread_t));

        printf("\nStart parallel computing...\n");
        start_time = clock();
        for (i = 0; i < THREAD_NUM; i++) {
            pthread_create(pthread_id + i, NULL, thread_sum, i);
        }
        for (i = 0; i < THREAD_NUM; i++) {
            pthread_join(pthread_id[i], NULL);
        }
        for (i = 0; i < THREAD_NUM; i++) {
            p_result += sum[i];
        }
        end_time = clock();
        p_time += (double)(end_time - start_time) / CLOCKS_PER_SEC;

        free(pthread_id);

        printf("\nSum of the array is %lld\n", p_result);
    }

    printf("\nRun for %d round(s), fetch %d everytime.\n", RND, FETCH_NUM);
    printf("Avg serial time cost: %lfs\n", s_time / RND);
    printf("Avg parallel time cost: %lfs\n", p_time / RND);
    printf("\nSpeedup: %lf\n", s_time / p_time);

    return 0;
}

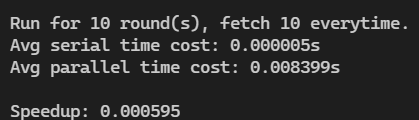
一次最多提取10个连续的数，更改 FETCH_NUM 为 10

#define FETCH_NUM 10

结果如下：

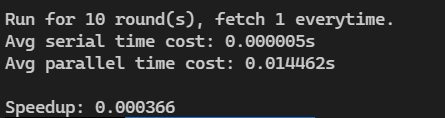
Pthreads 求解二次方程组的根

条件变量

条件变量是一个数据对象，允许线程在某个特定条件下或者时间按发生前都处于挂起状态。当事件或条件发生时，另一个线程都可以通过信号来唤醒挂起的线程。一个条件变量总是与一个互斥量相关联。

实现

// root_pthread.c

// Copyright (c) 2021 CHEN Yuhan
// Date: 2021-10-28
//

// Compile: gcc -pthread -lm -o root_p root_pthread.c
// Run:     ./root_p

#include <math.h>
#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define THREAD_NUM 4

pthread_mutex_t mutex;
pthread_cond_t  cond_var;

double a, b, c;
int    count;
double bb, four_ac, two_a, sqrtd, add, sub, a_d2a, s_d2a;

void *thread_root(void *arg) {
    int num_of_thread = (int)arg;
    printf("#%d start.\n", num_of_thread);

    pthread_mutex_lock(&mutex);
    count++;
    if (count == THREAD_NUM) {
        count   = 0;
        bb      = b * b;
        four_ac = 4 * a * c;
        printf("#%d computed b*b and 4ac.\n", num_of_thread);
        pthread_cond_broadcast(&cond_var);
    } else {
        while (pthread_cond_wait(&cond_var, &mutex))
            ;
    }
    pthread_mutex_unlock(&mutex);

    pthread_mutex_lock(&mutex);
    count++;
    if (count == THREAD_NUM) {
        count = 0;
        two_a = 2 * a;
        printf("#%d computed 2a.\n", num_of_thread);
        pthread_cond_broadcast(&cond_var);
    } else {
        while (pthread_cond_wait(&cond_var, &mutex))
            ;
    }
    pthread_mutex_unlock(&mutex);

    pthread_mutex_lock(&mutex);
    count++;
    if (count == THREAD_NUM) {
        count = 0;
        sqrtd = sqrt(bb - four_ac);
        printf("#%d computed sqrt.\n", num_of_thread);
        pthread_cond_broadcast(&cond_var);
    } else {
        while (pthread_cond_wait(&cond_var, &mutex))
            ;
    }
    pthread_mutex_unlock(&mutex);

    pthread_mutex_lock(&mutex);
    count++;
    if (count == THREAD_NUM) {
        count = 0;
        add   = -b + sqrtd;
        sub   = -b - sqrtd;
        printf("#%d computed -b +/-.\n", num_of_thread);
        pthread_cond_broadcast(&cond_var);
    } else {
        while (pthread_cond_wait(&cond_var, &mutex))
            ;
    }
    pthread_mutex_unlock(&mutex);

    pthread_mutex_lock(&mutex);
    count++;
    if (count == THREAD_NUM) {
        count = 0;
        a_d2a = add / two_a;
        s_d2a = sub / two_a;
        printf("#%d computed x1 and x2.\n", num_of_thread);
        pthread_cond_broadcast(&cond_var);
    } else {
        while (pthread_cond_wait(&cond_var, &mutex))
            ;
    }
    pthread_mutex_unlock(&mutex);

    printf("#%d exit.\n", num_of_thread);
    pthread_exit(0);
}
int main() {
    clock_t    start_time, end_time;
    pthread_t *pthread_id = NULL;
    long long  i;

    pthread_id = (pthread_t *)malloc(THREAD_NUM * sizeof(pthread_t));
    pthread_mutex_init(&mutex, NULL);
    pthread_cond_init(&cond_var, NULL);
    a = 1, b = 2, c = 0;
    for (i = 0; i < THREAD_NUM; i++) {
        pthread_create(pthread_id + i, NULL, thread_root, i);
    }
    for (i = 0; i < THREAD_NUM; i++) {
        pthread_join(pthread_id[i], NULL);
    }
    printf("\nx1=%lf\nx2=%lf\n", a_d2a, s_d2a);
    free(pthread_id);

    return 0;
}

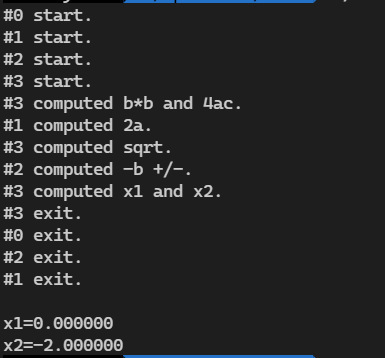
emmm，条件变量让这个并行程序有点像线程之间接力的串行程序，一开始想让 $b^2$ 和 $4ac$ 和 $2a$ 的计算并发，但是后来放弃了。

编译的时候加上 -lm 来使用 math.h 库

a=1 b=2 c=0 的结果

估算 $y=x^2$ 曲线与 x 轴之间区域的面积，其中 x 的范围为 [0,1]

Monte-carlo 方法就是统计模拟方法，用随机取点的概率来近似面积之比。在 x,y 属于 [0,1][0,1] 范围内任意取点，若在范围内则累计，最后与总数之比就可以近似面积之比。在多线程累加count的时候我使用了锁来防止竞争。

// root_pthread.c

// Copyright (c) 2021 CHEN Yuhan
// Date: 2021-10-28
//
// 估算 y=x^2 曲线与 x 轴之间区域的面积，其中 x 的范围为 [0,1] 。
// 在 x,y 属于 [0,1][0,1] 范围内任意取点，若在范围内则累计，
// 最后与总数之比就可以近似面积之比。

// Compile: gcc -pthread -lm -D_GNU_SOURCE -o mc_p Monte-carlo_pthread.c
// Run:     ./mc_p

// #ifndef __USE_GNU
// #define __USE_GNU
// #endif
// #ifndef _GNU_SOURCE
// #define _GNU_SOURCE
// #endif
#include <math.h>
#include <pthread.h>
#include <sched.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <unistd.h>

#define PROC_NUM 4
#define THREAD_NUM 4 // THREAD_NUM = PROC_NUM so 1 thread -> 1 processor
#define ROUND 10000000

int count;

double real_num = (double)1 / 3;

pthread_mutex_t mutex;

int inRange(double x, double y) {
    if (y <= x * x) return 1;
    return 0;
}

void *thread_func(void *arg) {
    int num_of_thread = (int)arg;
    printf("#%d start.\n", num_of_thread);

    cpu_set_t cpu_set;
    CPU_ZERO(&cpu_set);
    CPU_SET(num_of_thread % PROC_NUM, &cpu_set);
    sched_setaffinity(num_of_thread, sizeof(cpu_set), &cpu_set);

    double x, y;
    int    T           = ROUND / THREAD_NUM;
    int    local_count = 0;

    while (T--) {
        // Generate random point in [0, 1][0, 1].
        x = rand() / (double)RAND_MAX;
        y = rand() / (double)RAND_MAX;
		// judge if in range
        if (inRange(x, y)) local_count++;
    }

    pthread_mutex_lock(&mutex);
    count += local_count;
    pthread_mutex_unlock(&mutex);

    printf("#%d exit.\n", num_of_thread);
    pthread_exit(0);
}

int main() {
    long long i;
    pthread_mutex_init(&mutex, NULL);
    pthread_t *pthread_id = NULL;
    pthread_id            = (pthread_t *)malloc(THREAD_NUM * sizeof(pthread_t));

    for (i = 0; i < THREAD_NUM; i++) {
        pthread_create(pthread_id + i, NULL, thread_func, i);
    }

    for (i = 0; i < THREAD_NUM; i++) {
        pthread_join(pthread_id[i], NULL);
    }

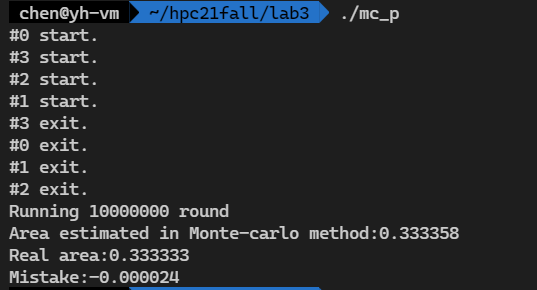
    printf("Running %d round\n", ROUND);
    printf("Area estimated in Monte-carlo method:%lf\n", (double)count / ROUND);
    printf("Real area:%lf\n", real_num);
    printf("Mistake:%lf\n", real_num - ((double)count / ROUND));

    free(pthread_id);

    return 0;
}

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

GEMM with Pthread