DCS293 - High Performance Computing 2021 Fall
DCS242 - Parallel and Distributed Computing 2021 Fall
背景
数学上,一个$m \times n$的矩阵是一个由$m$行$n$列元素排列成的矩形阵列。矩阵是高等代数中常见的数学工具,也常见于统计分析等应用数学学科中。通用矩阵乘法(GEMM)通常定义为:
$C=AB$
$C_{m,k}=\sum_{n=1}^{N}A_{m,n}B_{n,k}$
实现GEMM
输入:$M, N, K$ 三个整数(512~2048)
问题描述:随机生成$M*N$和$N*K$的两个矩阵$A$和$B$,对这两个矩阵做乘法得到矩阵$C$.
输出:$A,B,C$ 三个矩阵以及矩阵计算的时间
思路是首先根据输入分配三个矩阵的空间,然后随机生成数据填充$A, B$两个矩阵,然后根据 GEMM 的定义通过循环来计算结果。
核心代码有两部分,首先是生成矩阵,由于规定采用32位浮点,所以通过使用
0
A[m][n] = static_cast<float>(rand()) / (static_cast<float>(rand() / 100));
来生成浮点数。此处以$A$矩阵为例。
然后是GEMM,使用循环计算,时间复杂度是$O(MNK)$
0
1
2
3
4
5
6
7
8
9
10
···
// GEMM
for (m = 0; m < M; m++) {
for (k = 0; k < K; k++) {
C[m][k] = 0;
for (n = 0; n < N; n++) {
C[m][k] += A[m][n] * B[n][k];
}
}
}
···
全部代码在GEMMv1.cpp中。
计算结果:
0
1
2
3
chen@yh-vm:~hpc21fall/lab1$ ./a.out
Please input M, N and K!
1024 2048 666
Total time: 12.87s
使用Strasen算法进行优化
Volker Strassen 在 1969 年提出了复杂度为 $O(n^{\log_{2}7})$ 的矩阵乘算法。这是历史上第一次将矩阵乘的计算复杂度降低到$ O(n^3)$ 以下。
基于分治的思想,Starssen 算法将矩阵 $A,\ B,\ C \in R^{n^2 \times n^2}$ 分别拆分为更小的矩阵
\[\mathbf{A} = \begin{bmatrix} \mathbf{A}_{1,1} & \mathbf{A}_{1,2} \\ \mathbf{A}_{2,1} & \mathbf{A}_{2,2} \end{bmatrix},\\ \mathbf{B} = \begin{bmatrix} \mathbf{B}_{1,1} & \mathbf{B}_{1,2} \\ \mathbf{B}_{2,1} & \mathbf{B}_{2,2} \end{bmatrix},\\ \mathbf{C} = \begin{bmatrix} \mathbf{C}_{1,1} & \mathbf{C}_{1,2} \\ \mathbf{C}_{2,1} & \mathbf{C}_{2,2} \end{bmatrix}\]其中 $A_{i,j},\ B_{i,j},\ C_{i,j} \in R^{2^{n-1} \times 2^{n-1}}$ 。
根据矩阵基本的运算法则,拆分后朴素算法的计算如下所示,共需要八次小矩阵乘法和四次小矩阵加法计算。
\[\begin{align} \mathbf{C}_{1,1} &= \mathbf{A}_{1,1} \mathbf{B}_{1,1} + \mathbf{A}_{1,2} \mathbf{B}_{2,1} \\ \mathbf{C}_{1,2} &= \mathbf{A}_{1,1} \mathbf{B}_{1,2} + \mathbf{A}_{1,2} \mathbf{B}_{2,2} \\ \mathbf{C}_{2,1} &= \mathbf{A}_{2,1} \mathbf{B}_{2,1} + \mathbf{A}_{2,2} \mathbf{B}_{2,1} \\ \mathbf{C}_{2,2} &= \mathbf{A}_{2,1} \mathbf{B}_{2,2} + \mathbf{A}_{2,2} \mathbf{B}_{2,2} \end{align}\]分治本身并不能改进矩阵乘的计算效率,Strassen 引入了七个如下所示的用于辅助计算的中间矩阵
\[\begin{align} \mathbf{M}_{1} &:=\left(\mathbf{A}_{1,1}+\mathbf{A}_{2,2}\right)\left(\mathbf{B}_{1,1}+\mathbf{B}_{2,2}\right) \\ \mathbf{M}_{2} &:=\left(\mathbf{A}_{2,1}+\mathbf{A}_{2,2}\right) \mathbf{B}_{1,1} \\ \mathbf{M}_{3} &:=\mathbf{A}_{1,1}\left(\mathbf{B}_{1,2}-\mathbf{B}_{2,2}\right) \\ \mathbf{M}_{4} &:=\mathbf{A}_{1,2}\left(\mathbf{B}_{2,1}-\mathbf{B}_{1,1}\right) \\ \mathbf{M}_{5} &:=\left(\mathbf{A}_{1,1}+\mathbf{A}_{1,2}\right) \mathbf{B}_{2,2} \\ \mathbf{M}_{6} &:=\left(\mathbf{A}_{2,1}-\mathbf{A}_{1,1}\right)\left(\mathbf{B}_{1,1}+\mathbf{B}_{1,2}\right) \\ \mathbf{M}_{7} &:=\left(\mathbf{A}_{1,2}-\mathbf{A}_{2,2}\right)\left(\mathbf{B}_{2,1}+\mathbf{B}_{2,2}\right) \end{align}\]在得到这些中间矩阵的记过后,再将其组合得到最后的矩阵:
\[\begin{align} \mathbf{C}_{1,1} &=\mathbf{M}_{1}+\mathbf{M}_{4}-\mathbf{M}_{5}+\mathbf{M}_{7} \\ \mathbf{C}_{1,2} &=\mathbf{M}_{3}+\mathbf{M}_{5} \\ \mathbf{C}_{2,1} &=\mathbf{M}_{2}+\mathbf{M}_{4} \\ \mathbf{C}_{2,2} &=\mathbf{M}_{1}-\mathbf{M}_{2}+\mathbf{M}_{3}+\mathbf{M}_{6} \end{align}\]通过七次乘法和十八次加法,Strassen 算法将矩阵乘的算法复杂度降低到了 $O(n^{\log_{2}7})$ (递归地运行该算法)。
首先要求是边长为$2^n$的方阵,而现实生活中需要计算的矩阵并不一定都是符合规则的矩阵。我取大于等于输入的三个边的最小的$2^n$来作为三个矩阵补0之后形成的方阵的边长。在右下部分补0,计算出来的C矩阵右下部分也全部是0,可以略去取左上角$M*K$的子矩阵,就是最终的结果了。
实现主要是递归,在这里展示一下最开始的版本Strassen函数的伪代码
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
void Strassen(float** A, float** B, float** C, int R) {
// R 是此时输入的三个方阵的边长
int div2 = R / 2;
// 这里申请所需要的所有矩阵的空间,包括ABC的各四个子矩阵,七个辅助计算的中间矩阵,和两个临时矩阵。
···
// 这里通过两层循环遍历AB矩阵然后填充各四个子矩阵
for (int i = 0; i < div2; i++) {
for (int j = 0; j < div2; j++) {
A11[i][j] = A[i][j];
A12[i][j] = A[i][j + div2];
A21[i][j] = A[i + div2][j];
A22[i][j] = A[i + div2][j + div2];
B11[i][j] = B[i][j];
B12[i][j] = B[i][j + div2];
B21[i][j] = B[i + div2][j];
B22[i][j] = B[i + div2][j + div2];
}
}
// 接下来计算辅助计算矩阵
// M1
ADD(A11, A22, resA, div2);
ADD(A12, B22, resB, div2);
Strassen(resA, resB, M1, div2); // 递归计算
// M2
ADD(A21, A22, resA, div2);
Strassen(resA, B11, M2, div2); // 递归计算
···
// 接下来通过计算出来的辅助计算矩阵计算C的四个子矩阵
// C11d
ADD(M1, M4, resA, div2);
SUB(resA, M5, resB, div2);
ADD(resB, M7, C11, div2);
// C12
ADD(M3, M5, C12, div2);
// C21
ADD(M2, M4, C21, div2);
// C22
ADD(M1, M3, resA, div2);
SUB(M6, M2, resB, div2);
ADD(resA, resB, C22, div2);
// 最后合并C的四个子矩阵
for (i = 0; i < div2; i++) {
for (j = 0; j < div2; j++) {
C[i][j] = C11[i][j];
C[i][j + div2] = C12[i][j];
C[i + div2][j] = C21[i][j];
C[i + div2][j + div2] = C22[i][j];
}
}
// 释放空间
···
}
虽然不知道这七个辅助计算矩阵是怎么搞出来的,但是好在实现这个算法比较简单,程序也一下子就跑起来了。输入
0
1024 2048 666
计算结果如下:
0
Total time: 158.453s
比第一个实验实现的GEMM慢了十几倍!
在试验了以下几组数据之后,我发现了问题所在
0
1
2
1 1024 2
1023 1022 1024
1025 1024 1025
在第二个样例子中新的算法优化比较明显,而在第一和第三个样例中却形成了负优化。分析之后我认为,“补0”的操作在某些极端情况下极大加重了递归的深度导致了多运行了许多0与0之间的没必要的运算。
首先,在矩阵不大的情况下,直接使用GEMM会比递归稍微快一点,那能不能使递归在分到边长小于某个值的时候转而直接使用GEMM求出两个矩阵之积呢?于是代码改进如下:当三边最大长度大于128的时候才使用本算法,否则不补0直接使用GEMM;使用本算法的时候只补到边长的最大值,也就是不用在意是否是2的n次方,因为在分割到子矩阵边长小于64的时候也是直接使用GEMM完成矩阵乘法的计算,这样既可以避免过多补0,又可以避免递归过深,总而言之提升了效率。上面的伪代码修改如下:
0
1
2
3
4
5
6
7
8
9
10
11
void Strassen(float** A, float** B, float** C, int R) {
// R 是此时输入的三个方阵的边长
int div2 = R / 2;
// 这里申请所需要的所有矩阵的空间,包括ABC的各四个子矩阵,七个辅助计算的中间矩阵,和两个临时矩阵。
···
// 这里判断是否继续往下分割矩阵
if (div2 < STRASSEN_SIZE)
MUL(A, B, C, R, R, R);
else {
··· // 与上面一致
}
}
全部代码在GEMMv2.cpp。
优化后的计算结果:
0
Total time: 25.9435s
不过还是比GEMM慢了一倍,所以在遇到种不是很方的矩阵可能还是直接使用GEMM比较好一些。
但是在测试比较方的矩阵乘法时,优化就比较明显了。
0
1
2
3
4
5
6
7
chen@yh-vm:~hpc21fall/lab1$ ./v1.out
Please input M, N and K!
1025 1024 1023
Total time: 12.2561s
chen@yh-vm:~hpc21fall/lab1$ ./v2.out
Please input M, N and K!
1025 1024 1023
Total time: 4.61468s
随着矩阵越大,优化就越明显。
0
1
2
3
4
5
6
7
chen@yh-vm:~hpc21fall/lab1$ ./v1.out
Please input M, N and K!
2000 1898 2002
Total time: 147.423s
chen@yh-vm:~hpc21fall/lab1$ ./v2.out
Please input M, N and K!
2000 1898 2002
Total time: 35.7376s
基于软件优化的方法进行优化
除了从算法分析的角度优化通用矩阵乘,在实际的计算机系统中应用很多的还有软件优化的方法。软件优化方法基于对计算机体系机构和软件系统的特征分析,结合具体计算的特性,设计出针对性的优化方法。
循环拆分和向量化
首先将输出的计算拆分为 1×4 的小块,代码如下所示:
0
1
2
3
4
5
6
7
8
9
10
11
12
13
for (int m = 0; m < M; m++) {
for (int n = 0; n < N; n += 4) {
C[m][n + 0] = 0;
C[m][n + 1] = 0;
C[m][n + 2] = 0;
C[m][n + 3] = 0;
for (int k = 0; k < K; k++) {
C[m][n + 0] += A[m][k] * B[k][n + 0];
C[m][n + 1] += A[m][k] * B[k][n + 1];
C[m][n + 2] += A[m][k] * B[k][n + 2];
C[m][n + 3] += A[m][k] * B[k][n + 3];
}
}
}
由于一次循环计算中A矩阵使用的元素一致B矩阵中是四个连续的数,故我们可以将B矩阵中的一行四个数一起读入,减少访存次数。类似地,我们扩展到A矩阵,每次循环也计算四个元素,这样可以继续拆分成如下形式,每次计算一个4x4矩阵。
0
1
2
3
4
5
6
7
8
9
10
11
12
13
for (int m = 0; m < M; m += 4) {
for (int n = 0; n < N; n += 4) {
C[m + 0][n + 0..3] = 0;
C[m + 1][n + 0..3] = 0;
C[m + 2][n + 0..3] = 0;
C[m + 3][n + 0..3] = 0;
for (int k = 0; k < K; k++) {
C[m + 0][n + 0..3] += A[m + 0][k] * B[k][n + 0..3];
C[m + 1][n + 0..3] += A[m + 1][k] * B[k][n + 0..3];
C[m + 2][n + 0..3] += A[m + 2][k] * B[k][n + 0..3];
C[m + 3][n + 0..3] += A[m + 3][k] * B[k][n + 0..3];
}
}
}
进一步,我们可以将K维度拆分。
0
1
2
3
4
5
6
7
8
9
10
11
12
13
for (int m = 0; m < M; m += 4) {
for (int n = 0; n < N; n += 4) {
C[m + 0..3][n + 0..3] = 0;
C[m + 0..3][n + 0..3] = 0;
C[m + 0..3][n + 0..3] = 0;
C[m + 0..3][n + 0..3] = 0;
for (int k = 0; k < K; k += 4) {
C[m + 0..3][n + 0..3] += A[m + 0..3][k + 0] * B[k + 0][n + 0..3];
C[m + 0..3][n + 0..3] += A[m + 0..3][k + 1] * B[k + 1][n + 0..3];
C[m + 0..3][n + 0..3] += A[m + 0..3][k + 2] * B[k + 2][n + 0..3];
C[m + 0..3][n + 0..3] += A[m + 0..3][k + 3] * B[k + 3][n + 0..3];
}
}
}
接下来实现SIMD。我们注意到每次都是计算4个元素,自然想到了AVX等扩展向量指令集。有了向量指令集,访存和计算都可以向量化。因此我们可以再进一步,利用向量操作提高计算的性能。
这里的向量编号方式假定输入输出的内存布局都是行优先,那么两个输入各自的 16 个元素通过 4 次向量访存即可加载到寄存器中。由矩阵乘的规则可知,输入 A 中的行可一次性用作输出的计算,而输入 B 的行则要拆分使用。
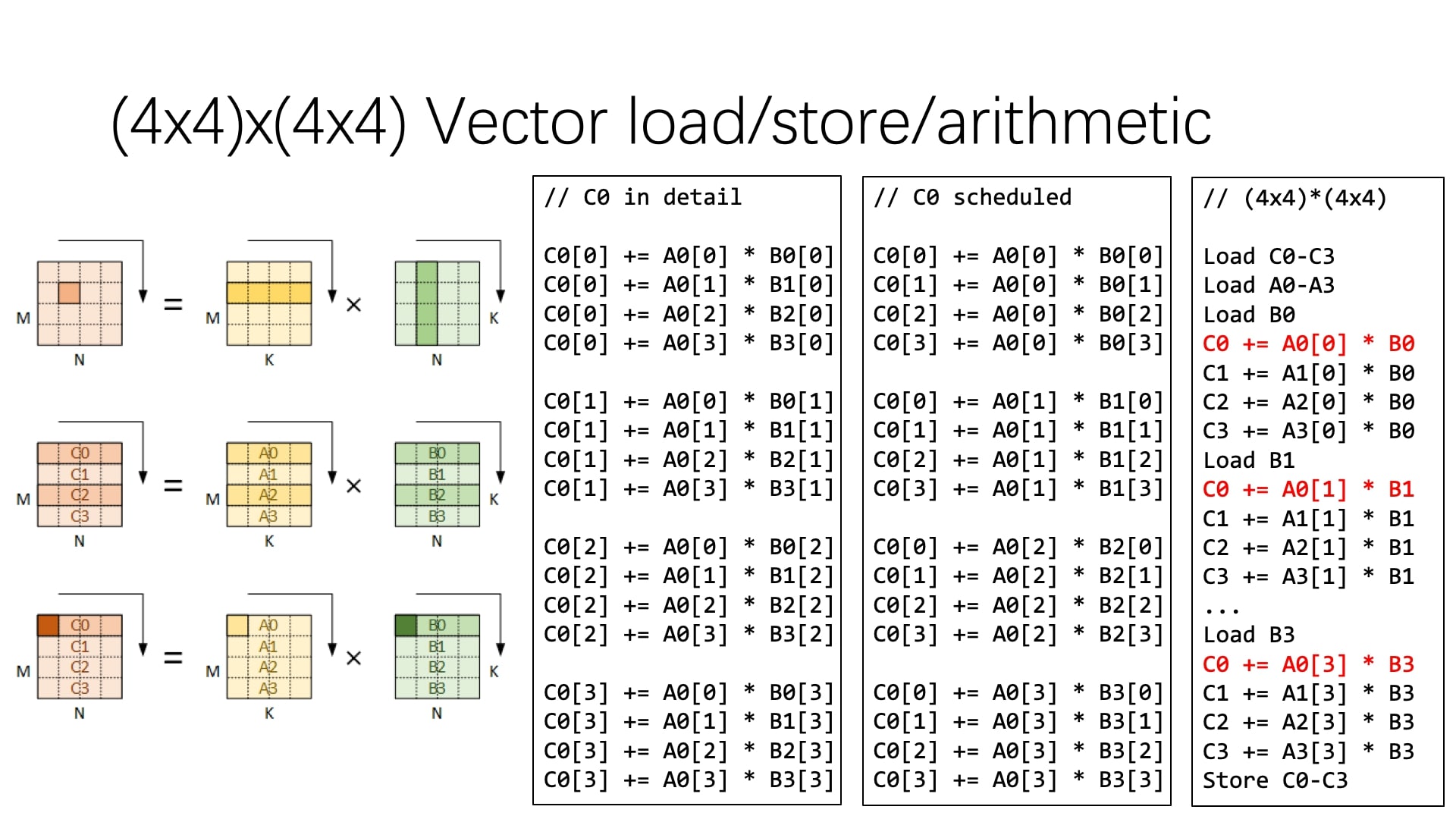
写代码的时候恰逢学习了 SSE/AVX 指令的使用和寄存器变量的使用。
AVX数据类型
| 数据类型 | 描述 |
|---|---|
| __m128 | 包含4个float类型数字的向量 |
| __m128d | 包含2个double类型数字的向量 |
| __m128i | 包含若干个整型数字的向量 |
| __m256 | 包含8个float类型数字的向量 |
| __m256d | 包含4个double类型数字的向量 |
| __m256i | 包含若干个整型数字的向量 |
由2个下划线开头,接一个m,然后是vector的位长度。
__m128,__m256每个数由4byte的float构成;
d后缀表示双精度浮点数,例如__m128d,__m256d,每个数由8byte的double构成。
__m128i,__m256i是由整型构成的向量,char,short,int,long均属于整型(以及unsigned以上类型),所以例如__m256i就可以由32个char,或者16个short,或者8个int,又或者4个long构成,这些整型可以是有符号类型也可以是无符号类型。
AVX函数
0
_mm<bit_width>_<name>_<data_type>
函数名称由_mm开头。
<bit_width> 表明了向量的位长度,对于128位的向量,这个参数为空,对于256位的向量,这个参数为256。
<name>描述了内联函数的算术操作。
<data_type> 标识函数主参数的数据类型,参数含义如下:
ps:里面都是float,把32bits当成一个数看pd:里面都是double,把64bits当成一个数看epi8/epi16/epi32/epi64:向量里每个数都是整型,一个整型8bit/16bit/32bit/64bitepu8/epu16/epu32/epu64:向量里每个数都是无符号整型(unsigned),一个整型8bit/16bit/32bit/64bitm128/m128i/m128d/m256/m256i/m256d:输入值与返回类型不同时会出现 ,例如__m256i_mm256_setr_m128i(__m128ilo,__m128ihi),输入两个__m128i向量 ,把他们拼在一起,变成一个__m256i返回 。另外这种结尾只见于loadsi128/si256:不care向量里到底都是些啥类型,反正128bit/256bit,例如:__m256i _mm_broadcastsi128_si256 (__m128i a)
AVX指令的函数可以通过Intrinsics Guide查询
寄存器变量
一般情况下,变量的值是存储在内存中的,CPU 每次使用数据都要从内存中读取。如果有一些变量使用非常频繁,从内存中读取就会消耗很多时间,例如 for 循环中的增量控制。为了解决这个问题,可以将使用频繁的变量放在CPU的通用寄存器中,这样使用该变量时就不必访问内存,直接从寄存器中读取,大大提高程序的运行效率。
0
register int i = 0; // 寄存器变量
关于寄存器变量有以下事项需要注意:
-
为寄存器变量分配寄存器是动态完成的,因此,只有局部变量和形式参数才能定义为寄存器变量
-
局部静态变量不能定义为寄存器变量,因为一个变量只能声明为一种存储类别。
-
寄存器的长度一般和机器的字长一致,所以,只有较短的类型如int、char、short等才适合定义为寄存器变量,诸如double等较大的类型,不推荐将其定义为寄存器类型。
-
CPU的寄存器数目有限,因此,即使定义了寄存器变量,编译器可能并不真正为其分配寄存器,而是将其当做普通的auto变量来对待,为其分配栈内存。当然,有些优秀的编译器,能自动识别使用频繁的变量,如循环控制变量等,在有可用的寄存器时,即使没有使用 register 关键字,也自动为其分配寄存器,无须由程序员来指定。
(这里最后没有用上寄存器变量)
单精度的实现
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
void my_mat_mul(int M, int N, int K, float **A, float **B, float **C) {
printf("M, N, K were expanded to %d, %d, %d\n\n", M, N, K);
for (int m = 0; m < M; m += 8) {
for (int k = 0; k < K; k += 8) {
__m256 C0v, C1v, C2v, C3v, C4v, C5v, C6v, C7v, B0v, B1v, B2v, B3v, B4v, B5v, B6v, B7v;
for (int n = 0; n < N; n += 8) {
C0v = _mm256_loadu_ps(&C[m][k]);
C1v = _mm256_loadu_ps(&C[m + 1][k]);
C2v = _mm256_loadu_ps(&C[m + 2][k]);
C3v = _mm256_loadu_ps(&C[m + 3][k]);
C4v = _mm256_loadu_ps(&C[m + 4][k]);
C5v = _mm256_loadu_ps(&C[m + 5][k]);
C6v = _mm256_loadu_ps(&C[m + 6][k]);
C7v = _mm256_loadu_ps(&C[m + 7][k]);
B0v = _mm256_loadu_ps(&B[n][k]);
C0v += A[m][n] * B0v;
C1v += A[m + 1][n] * B0v;
C2v += A[m + 2][n] * B0v;
C3v += A[m + 3][n] * B0v;
C4v += A[m + 4][n] * B0v;
C5v += A[m + 5][n] * B0v;
C6v += A[m + 6][n] * B0v;
C7v += A[m + 7][n] * B0v;
B1v = _mm256_loadu_ps(&B[n + 1][k]);
C0v += A[m][n + 1] * B1v;
C1v += A[m + 1][n + 1] * B1v;
C2v += A[m + 2][n + 1] * B1v;
C3v += A[m + 3][n + 1] * B1v;
C4v += A[m + 4][n + 1] * B1v;
C5v += A[m + 5][n + 1] * B1v;
C6v += A[m + 6][n + 1] * B1v;
C7v += A[m + 7][n + 1] * B1v;
...
B7v = _mm256_loadu_ps(&B[n + 7][k]);
C0v += A[m][n + 7] * B7v;
C1v += A[m + 1][n + 7] * B7v;
C2v += A[m + 2][n + 7] * B7v;
C3v += A[m + 3][n + 7] * B7v;
C4v += A[m + 4][n + 7] * B7v;
C5v += A[m + 5][n + 7] * B7v;
C6v += A[m + 6][n + 7] * B7v;
C7v += A[m + 7][n + 7] * B7v;
_mm256_storeu_ps(&C[m][k], C0v);
_mm256_storeu_ps(&C[m + 1][k], C1v);
_mm256_storeu_ps(&C[m + 2][k], C2v);
_mm256_storeu_ps(&C[m + 3][k], C3v);
_mm256_storeu_ps(&C[m + 4][k], C4v);
_mm256_storeu_ps(&C[m + 5][k], C5v);
_mm256_storeu_ps(&C[m + 6][k], C6v);
_mm256_storeu_ps(&C[m + 7][k], C7v);
}
}
}
}
双精度的计算结果:
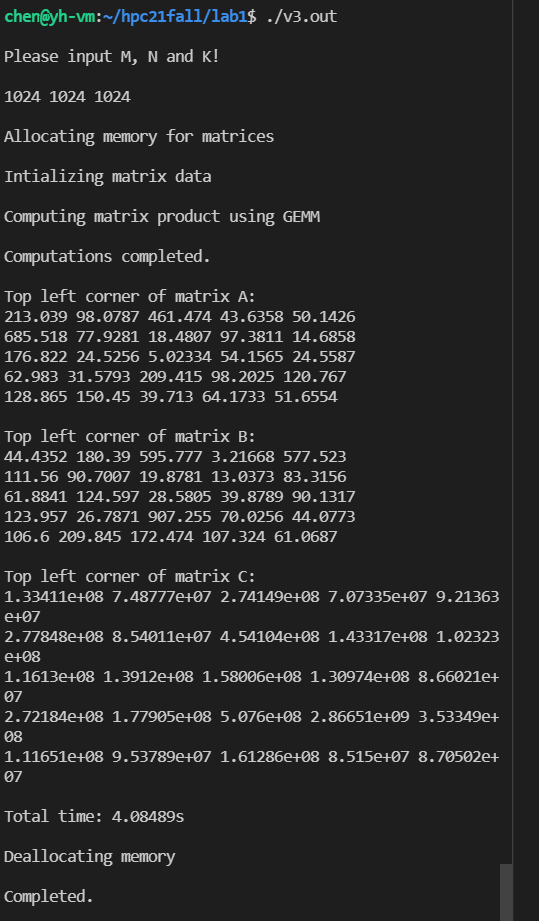
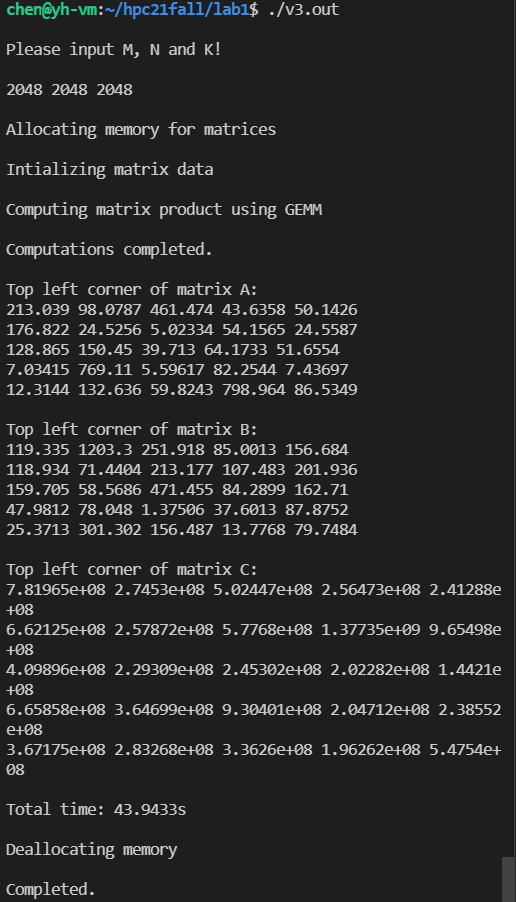
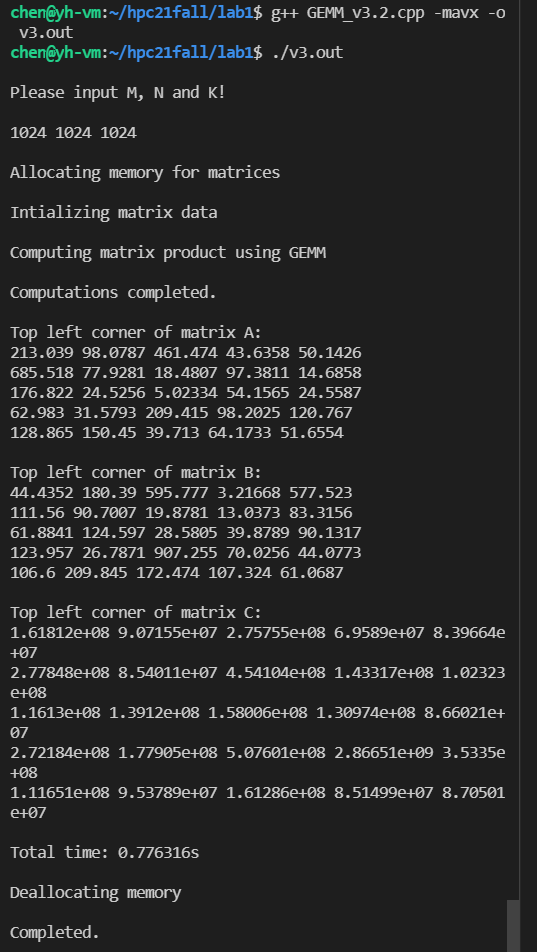
单精度(8x8)的计算结果:
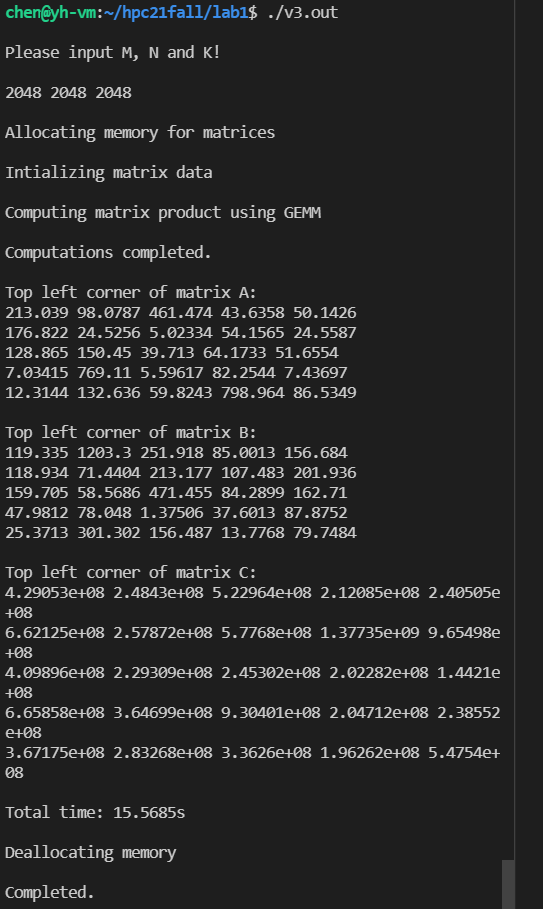
安装和使用 Intel® Math Kernel Library
Installing Intel® Performance Libraries and Intel® Distribution for Python* Using APT Repository
Using Intel® Math Kernel Library for Matrix Multiplication - C
MKL的示例代码中的define会报错
0
#define min(x,y) (((x) < (y)) ? (x) : (y))
修改为
0
#define MAX(x, y) (((x) > (y)) ? (x) : (y))#define MIN(x, y) (((x) < (y)) ? (x) : (y))
后便可以成功运行。
0
chen@yh-vm:~/hpc21fall/lab1$ g++ MKL_DGEMM.c -o test.o -I/opt/intel/mkl/include -I/opt/intel/mkl/lib/intel64 -I/opt/intel/lib/intel64 -lmkl_intel_lp64 -lmkl_core -lmkl_intel_thread -L/opt/intel/mkl/lib -I /opt/intel/compilers_and_libraries/linux/mkl/include -L /opt/intel/compilers_and_libraries/linux/mkl/lib -L /opt/intel/compilers_and_libraries/linux/lib -liomp5 -lpthreadchen@yh-vm:~/hpc21fall/lab1$ ./test.o
结果如下,在1s内。比起之前硬件优化后的35秒快了好多。
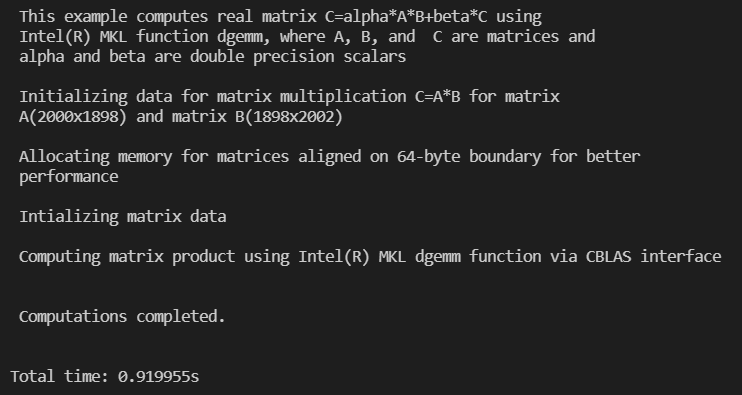
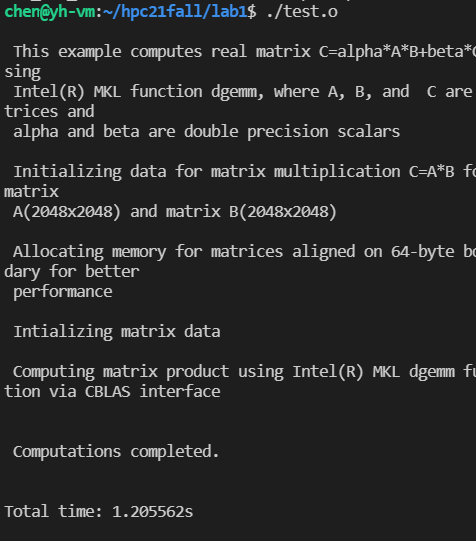
也比软件优化后快很多。
通过 Perf 工具分别观察以上方法性能
Perf
Perf 是一个基于 Linux 2.6 + 系统的分析工具,它抽象了在 Linux 中性能度量中 CPU 的硬件差异,提供一个简单的命令行界面。 Perf 基于最新版本 Linux 内核的perf_events 接口,提供了一组丰富的命令来收集和分析性能和跟踪数据。
我们来看看通过 perf stat 如何查看程序运行的一些指标。
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
chen@yh-vm:~/pdc21fall/hw2$ g++ GEMM_v1.cpp -o v1
chen@yh-vm:~/pdc21fall/hw2$ perf stat ./v1
Please input M, N and K!
300 300 300
Allocating memory for matrices
Intializing matrix data
Computing matrix product using GEMM
Computations completed.
Top left corner of matrix A:
213.039 98.0787 461.474 43.6358 50.1426
79.0461 82.471 101.143 325.695 132.728
170.134 148.651 65.4341 204.972 159.879
78.3836 74.5849 17.3884 160.906 15.4078
65.3493 105.441 79.2555 49.5163 259.583
Top left corner of matrix B:
151.745 250.309 75.4235 183.387 100.394
79.0114 44.8824 28.5541 90.0339 1.81483
173.621 390.892 181.111 97.8015 505.986
69.1606 14.6118 72.2107 123.116 100.722
134.801 729.928 233.94 1.37725 312.031
Top left corner of matrix C:
6.86743e+08 2.29095e+07 2.53445e+07 4.49561e+07 1.97556e+07
3.32926e+08 2.03221e+07 8.94079e+07 2.56722e+07 1.97053e+07
2.49845e+08 2.09325e+07 2.80914e+07 2.99431e+07 2.09396e+07
4.02668e+08 4.22321e+07 7.64501e+07 2.39132e+07 1.50527e+07
8.17621e+07 2.45983e+07 2.87312e+07 4.91162e+07 2.03496e+07
Total time: 0.236256s
Deallocating memory
Completed.
Performance counter stats for './v1':
256.32 msec task-clock # 0.066 CPUs utilized
5 context-switches # 0.020 K/sec
0 cpu-migrations # 0.000 K/sec
398 page-faults # 0.002 M/sec
525,752,068 cycles # 2.051 GHz
0 instructions # 0.00 insn per cycle
61,546,873 branches # 240.116 M/sec
191,341 branch-misses # 0.31% of all branches
3.900660630 seconds time elapsed
0.249214000 seconds user
0.007911000 seconds sys
这里出现一个问题,就是虚拟机开启了虚拟CPU计数器等后还是无法显示指令数,于是无法计算CPI。
或许可以使用Visual studio或者Windows Performance Toolkit,在Windows上测试。
总之,虽然在虚拟机上得不到CPI,我们可以直接通过时钟周期等其他参数来衡量性能。
循环测试并分析
单次实验具有偶然性,所以循环测试10次。矩阵大小 $300 \times 300$.
0
perf stat -e cpu-clock,context-switches,cpu-migrations,page-faults,cycles,instructions,L1-dcache-load-misses,mem_inst_retired.all_loads -r 10 ./v_1(/2/3)
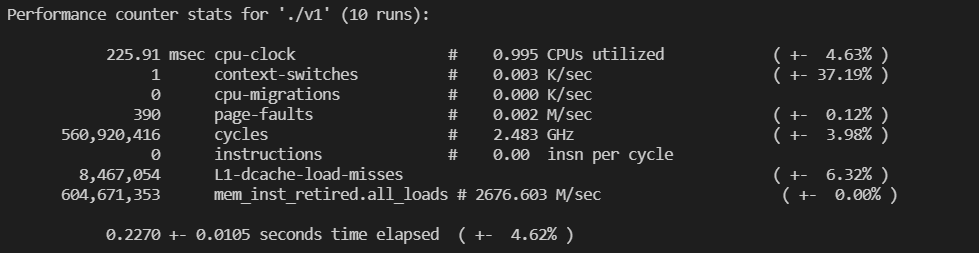
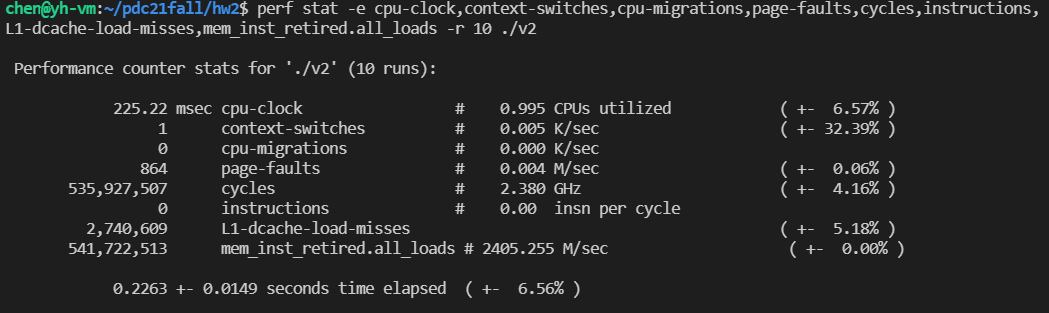
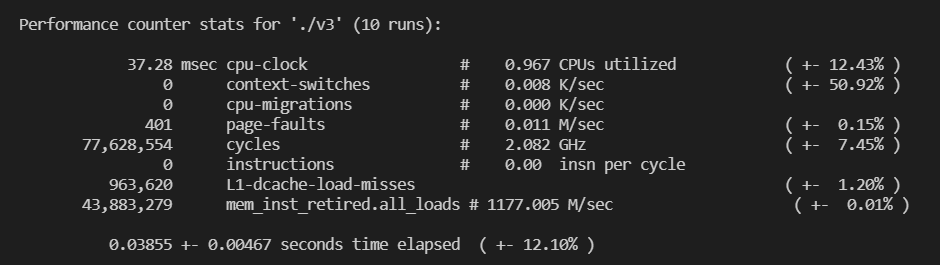
发现 Strassen 算法和一般算法一样快,这可能是矩阵规模不够大的缘故。而且,Strassen 算法的 cache miss 是一般算法的 1/3 以下。总共 CPU cycle 比一般算法略少。
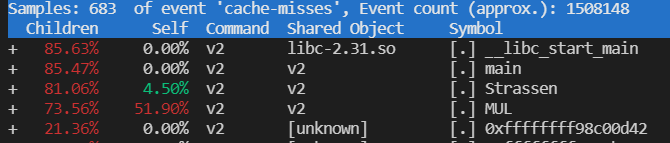
可以看出 Cache miss 一般发生在矩阵乘法过程中,所以由于Strassen 算法做了很多加减运算减少了矩阵乘法的运算。
使用循环拆分和向量化和 AVX 指令加速后的矩阵乘法需要的 CPU cycle 远少于上面两种算法,cache miss 也是 Strassen 算法的 1/3 ,mem_load 也远少于上面两种算法。且没有上下文切换。
继续阅读
References
使用Intel SSE/AVX指令集(SIMD)加速向量内积计算
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.


